String Gauge 101: Guide for Electric and Acoustic Guitar

Switching up your guitar’s string gauge is a good idea if you’re looking for a different tone and feel, and it’s one of the cheapest and easiest guitar modifications you can make. But which string gauge is best?

In this article, I’ll explain the different string gauges on offer for acoustic and electric guitars, the pros and cons of thick and thin strings and some overall recommendations for different guitar models.

What is String Gauge?

A guitar’s string gauge refers to the thickness measured as 1/1000th of an inch of the high E string. For example a set of 10-gauge strings will have a high E string with a thickness of 0.010 inches.

The best string gauge for most electric guitar players is either 9 or 10 gauge, and for acoustic guitars it is 12 gauge.

The sets use the high E string as a reference, which is the thinnest string in the set. Of course, the lower strings will be thicker. For example, a set of 10-gauge strings may also be called a 10-46 set, which means the low E string has a thickness of 0.046 inches.

Example: 10-gauge string set

• Low E: 0.046″
• A: 0.036″
• D: 0.026″
• G: 0.017″
• B: 0.013″
• High E: 0.010″

To make things simpler, the string sets are usually described as either super light, light, medium or heavy. These terms will vary depending on the brand and the guitar type (acoustic or electric).

There’s one rule to keep in mind, which affects everything the tone, tuning stability and playability of the gauges.

Thicker strings = More Tension

Now let’s take a look at the average gauges used on electric and acoustic guitars, before we jump into the pros and cons of thick and thin strings.

Average Electric Guitar String Gauges

On electric guitars, the most common string set is a 9-gauge set also know as a 0.009-0.042″ set. This is often referred to as a “light set” but is considered the average gauge, with many brands such as Fender, supplying their guitars with a 9-gauge string set.

Some brands such as Gibson and Epiphone supply a lot of their guitars, including the Les Paul with a 10-gauge string set which is refereed to as a “medium set”.

Electric guitar string sets vary from 8-gauge to 14-gauge, with the most common sets being the 9-gauge and 10-gauge sets. They are often referred to as either super light, light, medium and heavy, although some brands use different terms to describe them.

Here are some popular sets:

• Super light: 8-gauge or less (e.g. 8-38 set)
• Light: 9-gauge (e.g. 9-42 set)
• Medium: 10-gauge (e.g. 10-46 set)
• Heavy: 11-gauge or higher (e.g. 11-54 set)

Here is a list of the thickness of each string for the sets described above.

There can also be some variations, for example, some brands supply 10-gauge sets which go from 0.01″ to 0.046″, and others supply sets which go from 0.01″ to 0.048″. Although the examples listed above are the most common.

The only other variation, is for 7 and 8 string guitars. Typically, these guitars will use 10 gauge strings, so here are examples for 7 and 8 string variants.

Average Acoustic Guitar String Gauges

Most acoustic guitars have 12-gauge strings and are often supplied with this set as standard from the manufacturer. Acoustic string gauges can range from 9-gauge to 13-gauge to suit different playing styles and scale lengths, and to produce a different tone.

A set of 9s on an acoustic is pretty rate, and much more commonly seen on electric guitars, however, you can fit them with this gauge if you prefer. Generally, acoustic string sets come in 4 sizes: 10-gauge, 11-gauge, 12-gauge and 13-gauge.

Acoustic guitars usually use thicker gauge strings than electric guitars, because they produce a louder sound. Electric guitars generally use thinner strings to improve playability and because the extra volume is not needed as the guitar will be plugged into an amplifier.

Here are examples of acoustic guitar string gauge sets.

Thick vs Thin Strings

Now we’ve been through the basics, I wanted to talk about the differences between light and heavy gauge strings, to help you decide which will be best for you. Here are the categories I’ll be comparing them in:

• Guitar Suitability (scale length)
• Playability
• Tuning Stability
• Sound
• Music Style Suitability

Remember the key difference as we go through each category, thicker strings create more tension.

Guitar Suitability

One of the main reasons why there are so many different string gauges available, is to suit different guitars.

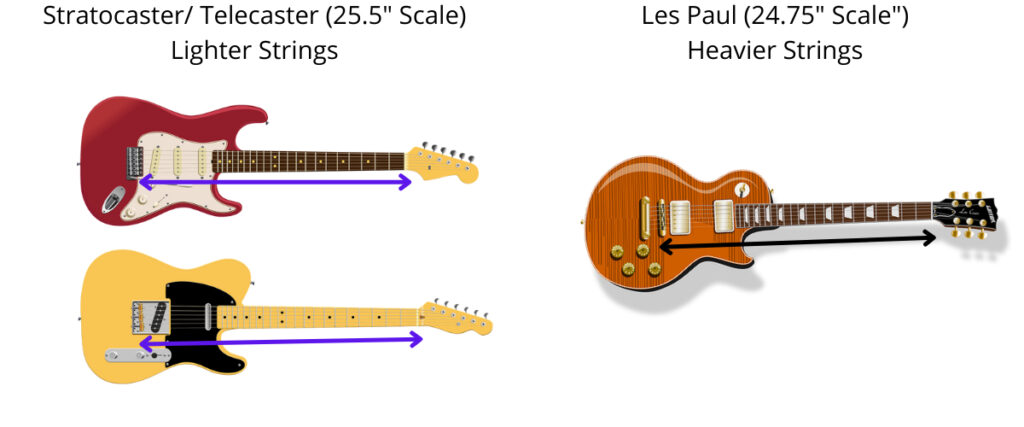
Different guitars have different scale lengths, which refers to the distance from the bridge to the nut of the guitar. For example, the Stratocaster and Telecaster have 25.5″ scale lengths, and the Les Paul has a 24.75″ scale length.

On guitars with a shorter scale length, the strings are under less tension. In order to compensate for the weaker tension, shorter scale guitars are often fitted with heavier gauge strings because they will create more tension.

For example, it’s common to use 10-gauge strings on a Les Paul, and 9-gauge on a Stratocaster or Telecaster.

Check out my article comparing 24.75″ and 25.5″ scale guitars to learn more.

Playability

String gauge has a big impact on how comfortable a guitar feels to play. Thicker (heavier gauge) strings, are harder to fret, and require more finger strength than thinner strings which are much easier to fret. Thinner strings also bend more easily and make the guitar feel “faster” to play.

Thicker strings create more tension, making them more difficult to hold for long periods, and perform bend. Often you’ll see older players who previously used thick strings, switch to light gauges because they are much less taxing on the fingers.

Consider your playing style when choosing the string gauge. If you’re a lead guitar player, then you may benefit from lighter strings that allow you to play more quickly and perform bends more easily, lending them well to soloing. If you’re a rhythm player, this is usually less of an issue, however, particularly thick strings may make barre chords more exhausting.

Tuning Stability and Drop Tuning

Another thing to keep in mind, is keeping your guitar in tune.

Lighter gauge strings tend to go out of tune more easily than heavier gauge strings. The thicker strings on a heavy gauge set create more tension, meaning it is more difficult to pull the guitar out of tune when playing. Whereas thin strings are more easily manipulated and stretched, leading to tuning instability.

If you’re using a set of 8s, and your guitar is constantly going out of tune, consider upping it to a set of 9s. But remember, it’s not the only factor to consider and there may be another issue causing your guitar to have tuning stability issues. Take your guitar to a good tech if you’re unsure and they’ll pinpoint the problem.

If you drop tune your guitar, thicker strings will be more suitable. Down-tuning a guitar will cause the strings to loosen and reduce the tension. Using heavier gauge strings creates more tension to help compensate, and will make the tone sound tighter and help the guitar stay in tune.

Sound Differences

Thicker strings sound louder than thinner strings. Heavy gauge strings (thick strings), produce more low-end frequencies (bass) which causes the increase in volume, and also makes the guitar sound warmer with more sustain. Lighter gauge strings do not sound as loud and typically have a brighter tone.

Although this difference in tone and volume is just one aspect to consider when choosing the string gauge, it does sometimes have an impact on the music styles they are used for.

For example, players who are looking to achieve a dark and heavy tone for metal, may select thicker strings. Whilst a player who wants to play cleaner tones and have a bright and chimey quality to the guitar for country, may prefer lighter strings.

However, I am a big believer that you shouldn’t just use thicker strings to get a different tone, if they don’t feel comfortable to you. Creating a good sound is more about your playing skills than it is about the string thickness. And remember, if you’re playing the electric guitar, you can use your amplifier to make tweaks to compensate, instead of using the string gauge to change the tone.

Here is a video where you can listen to the differences in tone between 8, 9, 10 and 11 gauge strings.

Music Style Suitability

This is where things start to come together. Different music styles require different playing skills and tunings. To demonstrate this point, I’ll use some examples.

If you’re a heavy metal player who often drop-tunes, uses a tremolo and plays heavy riffs and chords, then thicker strings are likely to be more suitable. The extra tension will help the guitar stay in tune, and the thicker strings will produce a heavier tone with more low-end.

However, if you’re a heavy metal lead player, and you are constantly shredding or bending strings, lighter strings may be more suitable. Lighter strings will make it easier to play quickly and perform technically difficult skills more easily than thicker strings.

Which String Gauge Should You Choose?

So which gauge strings should you get?

Well, it’s is all personal preference, and it’s best to try out some different gauges every time you change your strings, in order to find the set that best suits you and your guitar.

When making a decision, consider these factors in the following order (highest to lowest priority)

• Playability
• Guitar Scale Length
• Tuning stability
• Tone

Here’s a table to summarise the pros and cons of thick and thin strings.

Heavy Gauge (Thick Strings)	Light Gauge (Thin Strings)
Create more tension	Create less tension
Better tuning stability	Go out of tune more easily
Suit shorter scale length guitars	Suit longer scale length guitars
Louder	Quieter
Harder to play	Easier to play
Better for drop tuning	Suited to standard tuning
Less prone to fret buzz	More prone to fret buzz
Strings are harder to snap	Strings snap more easily

As I said, it’s best to experiment.

For example, my PRS SE Custom 24 came with 9-gauge strings. It has a 25″ scale length which is fairly standard, but my bends felt a bit wild and I pulled the guitar out of tune a little too often. I switched to 10-gauge strings and found them perfect. They weren’t too tough on my fingers, and my bends felt more controlled, so I’ve stuck with them.

Don’t be extreme and go all the way from 8-gauge to 13-gauge strings in one string change, but going up or down one level is a great idea if you’ve only every tried one gauge before.

Mixing String Gauges (Hybrid Sets)

One way to combat the conflict between the pros and cons light and heavy strings, is to use a hybrid set. For example, a light top/ heavy bottom set. Take this as an example.

Here you can set that on the hybrid set, the Low E, A and D strings are heavier than on a typical 10-gauge set. So what’s the point in this?

Well, the higher strings are often used for soloing, bending strings and general lead playing, so having thinner strings makes this a lot easier. The low string which are often used for power chords, will benefit from the extra tuning stability. So essentially, you get the best of both worlds!

Here are some more articles you might find useful:

• 4 Ways a Guitar’s Strings Affect its Tone
• 6 Ways to Make a Cheap Electric Guitar Sound Great